Exploring Work & Energy in HSC Physics
Introducing the concepts of Work and Energy in relation to Advanced Mechanics, part of Module 5
Defining work
Work is a measure of the displacing effect of a force on an object. It is found by multiplying the applied force with the displacement travelled in the direction of the applied force. Quantitatively: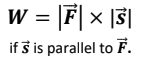
It should be noted that whilst force and displacement are both vector quantities, work is a scalar quantity.
Defining energy
Energy is defined as the capacity to do work. It is measured in joules. Conversely, work can be considered a transfer of energy between objects.
The net work done on an object is equal to the change in energy of said object:
Talent tip: Questions tend to ask for the work done on an object, and this work can either be positive or negative. If it is positive, then this object is having work done on it. If it is negative, then this object is doing work.
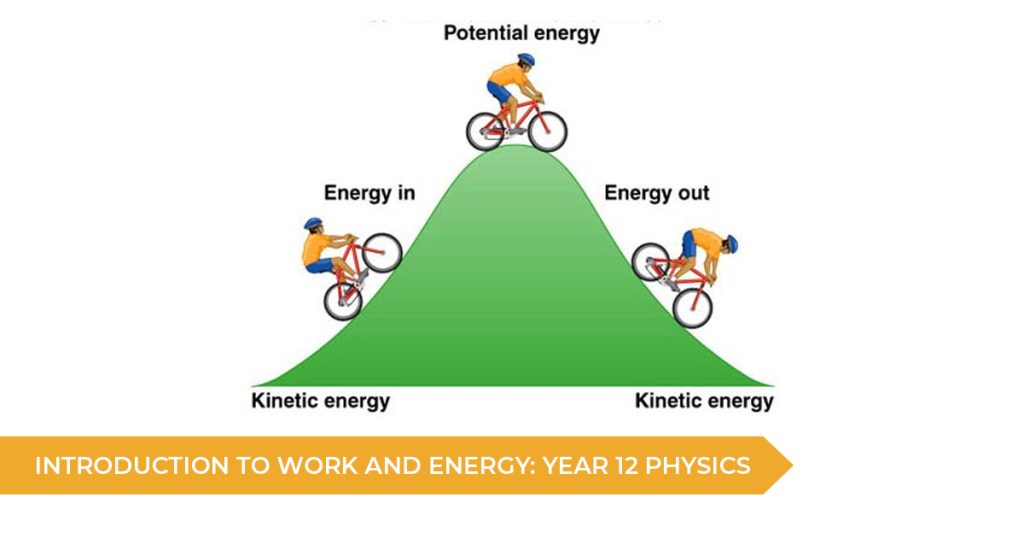
Kinetic Energy
Kinetic energy is the energy possessed by an object because it is moving. Since moving objects can collide with other objects and in doing so apply a force on them (and thus do work on them), they must possess a type of energy. An object’s kinetic energy is dependent on both its speed and its mass. Quantitatively this relationship can be described as below: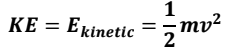
Potential Energy
Potential energy is a difficult concept to grasp. In this course we will primarily learn about gravitational potential energy and electric potential energy. Both of these forms of potential energy arise from an object’s position in a field.
RELATED: Using The HSC Physics Formula Sheet
Potential energy can be more easily understood using the concept of work. Let us look at the following example:
An apple is picked up off the ground and lifted to a height of 1m. At all times the apple is experiencing a downwards force towards the ground due to gravity. To overcome this weight force, an upwards force on the apple has gained energy as a direct result of its position above the ground. This energy is the gravitational potential energy of the apple.
Quantitatively we can determine the potential energy of an object in a field, calculating the work required to place it there. This requires the use of Newton’s 2nd Law of Motion, and yields the following two equations for gravitational and electric potential energy.
Gravitational Potential Energy
Where EPE = electric potential energy, q= charge of object, E= electric field, d= distance of object from the ‘attractive’ source of the electric field. This is assuming that the electric field strength is constant.
Talent tip: When the force is not uniform, a different formula is required to determine the potential energy. These equations will be taught later in this course, and their derivations require the use of integration.